DANA
Industrial Drive Shafts Catalogue
| Drive Shafts | |
|
|
| General fundamental theory | ||
| tt back to Table of contents | ||
| Kinematics of Hooke's joints
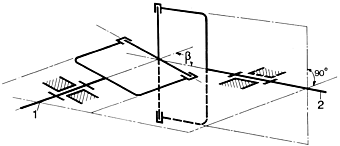
1. The joints In the theory of mechanics the cardan joint or Hooke's joint is defined as a spatial or spherical drive unit with a non-uni form gear ratio or transmission. The transmission behaviour of this joint is described by the equation. |
||
  |
||
In this equation  the momentary rotation angle of the driven
shaft 2. The motion behaviour of the driving and the
driven ends is shown in the following diagram. The
asynchronous and / or non-homokinematic running of the
shaft 2 is shown in the periodical oscilation of the
asynchronous line round the synchronous line
 (dotted line). |
||
 |
||
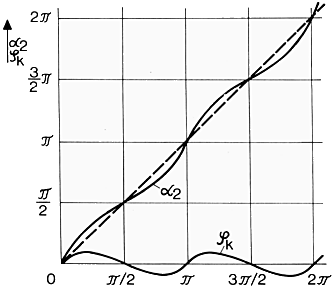
A measure for the non-uniformity is the
difference of the rotation angles
and
or the transmission ratio of the angular
speeds  and
 . |
||
Expressed by an equation, that means:
|
 a) rotation angle difference (also called gimbal error) 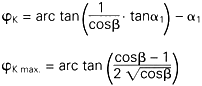 b) Gear ratio  |
|
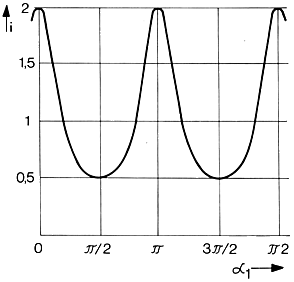
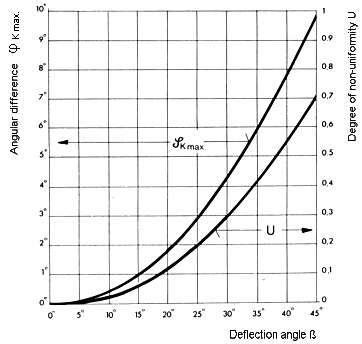
The following diagram shows the gear ratio i = /
for a full revolution of the universal joint
for β = 60°. |
 |
|
|
The degree of non-uniformity U is
defined by: U = i max. - i min. = tan β * sin β where:  |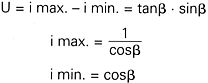
||
 |
||
The diagram shows the course of the
degree of nonuniformity U and of the angular difference
 as a function of the deflection angle of the
joint from 0 to 45°.From the motion equation it is evident that a homokinematic motion behaviour corresponding to the dotted line under 45° - as shown in the diagram - can only be obtained for the deflection angle β = 0°. A synchronous or homokinematic running can be achieved by a suitable combination or connection of two or more joints. |
||
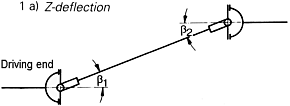
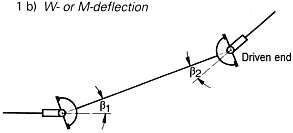
| 2. The universal shaft The rotation angle difference  or the gimbal error of a deflected universal
joint can be offset under certain installation conditions
with a second universal joint. The constructive solutions
are the following: 1) The deflection angles of both joints must be equal, i.e.  Two arrangements are possible: |
||
 |
||
 |
||
2) The two joints must have a kinematic
angular relationship of 90° (
/ 2), i.e. the yokes of the connecting shaft are in one
plane. For a more intensive study of universal shaft kinematics we refer you to the VDI-recommendation 2722 to the relevant technical literature. |
||
| tt back to Table of contents | ||
| Email : info@landmark-autoparts.com | Websites |
|